BP
21 July 2014 编辑本文
Theorectical relationship between back-projection imaging …
$$
F_{cut} \thickapprox \frac{1}{4}\frac{V_s}{\Delta}
$$
$$
\begin{aligned}
\frac{D_i(\omega)}{G_{ij}(\omega)}&=\frac{G_{ik}(\omega)S_k(\omega)}{G_{ij}(\omega)}=S_j(\omega)+\sum_{j\neq k}\frac{G_{ik}}{G_{ij}}\cdot S_k(\omega) \\
\mathbb{S_j}(t)&=S_j(t)+\sum_{j\neq k} \delta_k(t) * S_k(t) \\
\textit{with:} & \qquad \delta_k(t)*G_{ij}(t)=G_{ik}(t) \\
~ & ~\\
&=S_j(t)+\sum_{j\neq k} S_k(t+\frac{\Delta L_{jk} \cos \theta}{V_p}) \\
Tr_k-Tr_j&=\frac{\Delta L}{Vr} \\
\Delta t &= \frac{\Delta L}{Vr} - \frac{\Delta L \cos \theta}{V_p}
\end{aligned}
$$
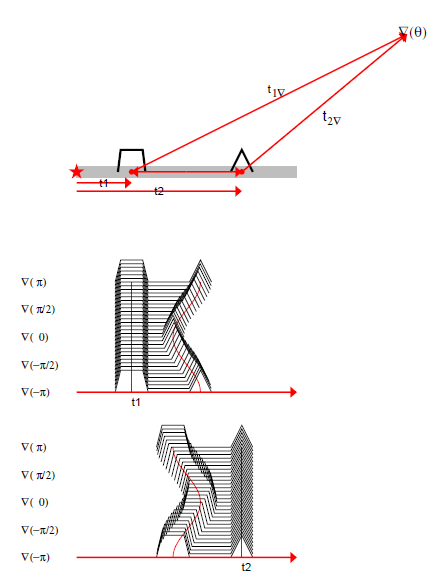
Time reversal
$$
\begin{aligned}
S_l^{TR}(t)&=\sum_k S_{lk}^{TR}(t)=\sum_k c_k'' \int_{-\infty}^{\infty} d_k(t_0-\tau) \widetilde
G_{lk}(t-\tau)~d\tau \\
\\
d_k^{TR}(t)&=d_k(t_0-t) \\
S_{lk}^{TR}(t) &\propto d_k^{TR}(t)*G^s_{lk}(t) \\
\\
G^s_{lk}(t)& \approx A^s_{lk}\delta(t-t^p_{kl}) \\
G^d_{lk}(t)& \approx A^d_{lk}\delta(t-t^p_{kl}) \\
\\
d_k(t) ~ &= \sum_l S_l(t)* G^d_{lk}(t) \\
~ &= \sum_l A^d_{kl}*S_l(t-t_{kl}^p) \\
d_k^{TR}(t) ~ & = \sum_l A^d_{kl}*S_l(t_0-t-t_{kl}^p) \\
S_{lk}^{TR}(t) &= c_k'' d_k^{TR}(t)*G_{lk}^s(t) \\
&= c_k'' \sum_l c \cdot S_l(t_0-t+t_{kl}^p-t_{kl}^p) \\
&\propto S_l(t_0-t) \\
\end{aligned}
$$
