ABIC0

$$ min: \left(d-Ha\right)^T E^{-1} (d-Ha) $$

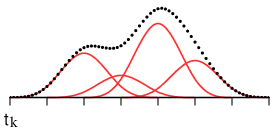
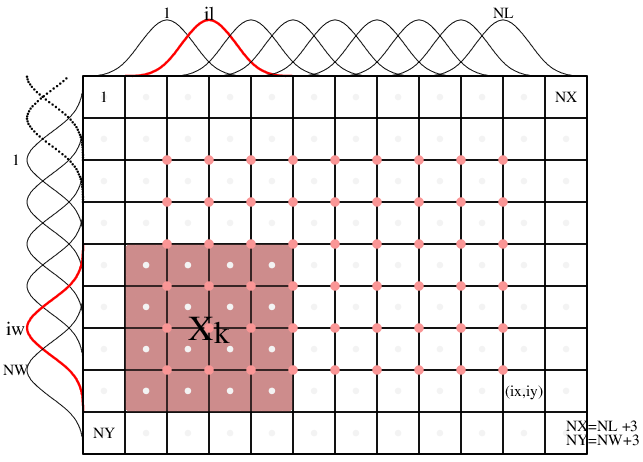
$$ \begin{aligned} u_j\left(t\right) &= \sum_{q=1}^2 \int_s G_{qj}^0\left(t,\xi\right)*\dot{D}_q^0\left(t,\xi\right)~d\xi +e_{bj}\left( t \right) \\ \dot{D}_q^0\left(t,\xi\right) &\thickapprox \sum_{k=1}^K \sum_{l=1}^L a_{qkl}X_k\left(\xi\right)T_l\left(t-t_k\right) \end{aligned} $$

$$ \begin{aligned} u_j(t)&=\sum_{q=1}^2 \int_s G_{qj}^0\left(t,\xi\right)*{\color{red}\dot{D}_q^0\left(t,\xi\right)} ~d\xi + e_{bj}\left( t \right) \\ &\thickapprox\sum_{q=1}^2 \int_s G_{qj}^0\left(t,\xi\right)*{\color{red}\sum_{k=1}^K \sum_{l=1}^L a_{qkl}X_k(\xi)T_l\left(t-t_k\right)} ~d\xi +e_{bj}(t)\\ &=\sum_{q=1}^2 \sum_{k=1}^K \sum_{l=1}^L a_{qkl} T_l \left(t-t_k\right) * {\color{red}\int_s X_k\left(\xi\right)G_{qj}^0\left(t,\xi\right) ~d\xi} +e_{bj}(t)\\ &=\sum_{q=1}^2 \sum_{k=1}^K \sum_{l=1}^L a_{qkl} T_l \left(t-t_k\right) * \left[{\color{red}\int_s X_k \left(\xi\right)G_{qj}\left(t,\xi\right) ~d\xi + \delta g_{qkj}(t)}\right] +e_{bj}(t) \\ &=\sum_{q=1}^2 \sum_{k=1}^K \left[ \sum_{l=1}^L T_l \left(t-t_k\right) * \int_s X_k \left(\xi\right)G_{qj}\left(t,\xi\right) ~d\xi ~ {\color{red}a_{qkl}}+ \sum_{l=1}^L a_{qkl} ~ T_l \left(t-t_k\right) * {\color{red}\delta g_{qkj}(t)}\right] +e_{bj}( t ) \\ &=\left[ \sum_{q=1}^2 \sum_{k=1}^K\sum_{l=1}^L\bbox[#eee]{ T_l (t-t_k) * \int_s X_k(\xi)G_{qj}(t,\xi) ~d\xi} ~ {\color{red}a_{qkl}} \right] +\left[ \sum_{q=1}^2 \sum_{k=1}^K\bbox[#eee]{\sum_{l=1}^L a_{qkl} ~ T_l(t-t_k)}*{\color{red}\delta g_{qkj}(t)} +e_{bj}(t) \right] \\ &=\left[ \sum_{q=1}^2 \sum_{k=1}^K\sum_{l=1}^L\bbox[#eee]{\widetilde{H}_{qklj}(t)} ~ {\color{red}a_{qkl}} \right] +\left[ \sum_{q=1}^2 \sum_{k=1}^K\bbox[#eee]{\widetilde{P}_{qk}\left(t,a_{qkl}\right)}*{\color{red}\delta g_{qkj}(t)} +e_{bj}(t) \right] \\ \textit{if:}\quad & \int_s X_k \left(\xi\right)G_{qj}(t,\xi) ~d\xi \thickapprox \int_s X_k (\xi)G_{qj}(t,\xi_k) ~d\xi =G_{qkj}(t)\cdot\Delta \xi_1 \Delta \xi_2 ;\quad \textit{GRN instead from 16 grids}\\ &=\left[ \sum_{q=1}^2 \sum_{k=1}^K\sum_{l=1}^L\bbox[#eee]{ T_l (t-t_k) * G_{qkj}(t)\cdot\Delta \xi_1 \Delta \xi_2 } ~ {\color{red}a_{qkl}} \right] +\left[ \sum_{q=1}^2 \sum_{k=1}^K\bbox[#eee]{\sum_{l=1}^L a_{qkl} ~ T_l(t-t_k)}*{\color{red}\delta G_{qkj}(t)\cdot\Delta \xi_1 \Delta \xi_2 } +e_{bj}(t) \right] \\ \textit{if:}\quad & X_k \textit{boxcar instead of B-spine}\\ &=\left[ \sum_{q=1}^2 \sum_{k=1}^K\sum_{l=1}^L\bbox[#eee]{ T_l (t-t_k) * G_{qkj}(t)\cdot\Delta \xi_1 \Delta \xi_2 } ~ {\color{red}a_{qkl}} \right] +\left[ \sum_{q=1}^2 \sum_{k=1}^K\bbox[#eee]{\sum_{l=1}^L a_{qkl} ~ T_l(t-t_k)}*{\color{red}\delta G_{qkj}(t)\cdot\Delta \xi_1 \Delta \xi_2 } +e_{bj}(t) \right] \\ d_j(t)&=B(t)*u_j(t) \qquad \textit{with: FIR implemented by convolution,} B(t) \\ &\thickapprox\left[ \sum_{q=1}^2 \sum_{k=1}^K\sum_{l=1}^L\bbox[#eee]{B(t)*\widetilde{H}_{qklj}(t)}~{\color{red}a_{qkl}} \right] +\left[ \sum_{q=1}^2 \sum_{k=1}^K\bbox[#eee]{B(t)*\widetilde{P}_{qk}\left(t,a_{qkl}\right)}*{\color{red}\delta g_{qkj}(t)} +B(t)*{\color{red}e_{bj}(t)} \right] \\ &=\left[ \sum_{q=1}^2 \sum_{k=1}^K\sum_{l=1}^L\bbox[#eee]{H_{qklj}(t)} ~ {\color{red} a_{qkl}} \right] +\left[ \sum_{q=1}^2 \sum_{k=1}^K\bbox[#eee]{P_{qk}\left(t,a_{qkl}\right)}*{\color{red}\delta g_{qkj}(t)}+B(t)*{\color{red}e_{bj}(t)}\right] \\ &=\left[ \sum_{q=1}^2 \sum_{k=1}^K\sum_{l=1}^L\bbox[#eee]{B(t)*T_l(t-t_k)*\int_s X_k(\xi)G_{qj}(t,\xi) ~d\xi } ~ {\color{red}a_{qkl}}\right] +\left[ \sum_{q=1}^2 \sum_{k=1}^K\bbox[#eee]{\sum_{l=1}^L a_{qkl}~B(t)*T_l(t-t_k)}*{\color{red}\delta g_{qkj}(t)}+B(t)*{\color{red}e_{bj}(t)}\right] \\ &=\mathbb{B}~u_j(t) \qquad \textit{with: IIR implemented by difference equation,}\mathbb{B} \\ &\thickapprox\left[ \sum_{q=1}^2 \sum_{k=1}^K\sum_{l=1}^L\bbox[#eee]{\mathbb{B}~\left[T_l(t-t_k)*\int_s X_k(\xi)G_{qj}(t,\xi) ~d\xi\right] } ~ {\color{red}a_{qkl}}\right] +\left[ \sum_{q=1}^2 \sum_{k=1}^K\bbox[#eee]{\sum_{l=1}^L a_{qkl}~T_l(t-t_k)}*{\color{red}\delta g_{qkj}(t)}+{\color{red}e_{bj}(t)}\right] \\ \end{aligned} $$

$$ \begin{aligned} 24 \Delta s^4 M_{4,j+2}\left( s \right) &= \begin{cases} \frac{1}{8}\Delta s^3 &; s=s_j-1.5\Delta s &; \frac{\int (\cdots) ~ds}{\Delta s} = \frac{1}{4}\Delta s^3 \\ \frac{23}{8}\Delta s^3 &; s=s_j-0.5\Delta s &; \frac{\int (\cdots) ~ds}{\Delta s} = \frac{11}{4}\Delta s^3 \\ \frac{23}{8}\Delta s^3 &; s=s_j+0.5\Delta s &; \frac{\int (\cdots) ~ds}{\Delta s} = \frac{11}{4}\Delta s^3 \\ \frac{1}{8}\Delta s^3 &; s=s_j+1.5\Delta s &; \frac{\int (\cdots) ~ds}{\Delta s} = \frac{1}{4}\Delta s^3 \\ \end{cases} \\ \end{aligned} $$

$$ \begin{matrix} \frac{\Delta \xi_1 \Delta \xi_2 }{576}&\frac{1}{24}\Delta \xi_1&\frac{11}{24}\Delta \xi_1 &\frac{11}{24}\Delta \xi_1 &\frac{1}{24}\Delta \xi_1 \\ \frac{1 }{24}\Delta \xi_2 & 1 & 11 & 11 & 1\\ \frac{11}{24}\Delta \xi_2 & 11 & 121 & 121 & 11\\ \frac{11}{24}\Delta \xi_2 & 11 & 121 & 121 & 11\\ \frac{1 }{24}\Delta \xi_2 & 1 & 11 & 11 & 1\\ \end{matrix} $$

$$ \begin{aligned} e_j(\mathbf{a})&=\left[ \sum_{q=1}^2 \sum_{k=1}^K\bbox[#eee]{\widetilde{P}_{qk}\left(t,a_{qkl}\right)}*{\color{red}\delta g_{qkj}(t)} +e_{bj}(t) \right] \\ &=\left[ \sum_{q=1}^2 \sum_{k=1}^K\bbox[#eee]{\sum_{l=1}^L a_{qkl}~T_l(t-t_k)}*{\color{red}\delta g_{qkj}(t)}+{\color{red}e_{bj}(t)}\right] \end{aligned} $$

$$ P_{qk}(t,a_{qkl}) \ast \delta g_{qkj}(t) \iff \begin{bmatrix} p_1 & 0 & \ldots & 0 & 0 \\ p_2 & p_1 & \ldots & \vdots & \vdots \\ p_3 & p_2 & \ldots & 0 & 0 \\ \vdots & p_3 & \ldots & p_1 & 0 \\ p_{m-1} & \vdots & \ldots & p_2 & p_1 \\ p_m & p_{m-1} & \vdots & \vdots & p_2 \\ 0 & p_m & \ldots & p_{m-2} & \vdots \\ 0 & 0 & \ldots & p_{m-1} & p_{m-2} \\ \vdots & \vdots & \vdots & p_m & p_{m-1} \\ 0 & 0 & 0 & \ldots & p_m \end{bmatrix} \begin{bmatrix} g_1 \\ g_2 \\ g_3 \\ \vdots \\ \vdots \\ \vdots \\ g_{n_j} \end{bmatrix} $$

$$ \begin{aligned} \mathbf{C}_{dj}(\sigma_g^2,\sigma_b^2,\mathbf{a})=& {\color{gray} \sigma_g^2\sum_{q=1}^{2}\sum_{k=1}^K S^2_{qkj}\mathbf{P}_{qkj}(\mathbf{a})\mathbf{P}_{qkj}^T(\mathbf{a}) + \sigma_b^2 O_{bj}^2\mathbf{B}_j\mathbf{B}_j^T } \\ \iff & \sigma_g^2\sum_{q=1}^{2}\sum_{k=1}^K\mathbf{P}_{qkj}(\mathbf{a})\mathbf{S}_{qkj}^2\mathbf{P}_{qkj}^T(\mathbf{a})+\sigma_b^2 \mathbf{O}_{bj}^2 \end{aligned} $$

$$ \bbox[margin:0px -20px 0px 0px ; padding-bottom:5px]{ \begin{matrix} ~ & \mathbf{ \bbox[padding:23px; border:2px solid black] { S_\xi } } \\ & \mathbf{ \bbox[padding:23px; border:2px solid black] { S_\tau} } \end{matrix} } \mathbf{\bbox[padding:25px 2px; border:2px solid black] {a}} = \begin{matrix} \mathbf{\bbox[padding:25px 2px; border:2px solid black] {0}} & \sim ~ \rho_\xi^2\\ \mathbf{\bbox[padding:25px 2px; border:2px solid black] {0}} & \sim ~ \rho_\tau^2 \end{matrix} $$

$$ \begin{aligned} \mathbf{d-Ha} & \sim (\mathbf{0}, \mathbf{C_d} ) \\ \mathbf{Sa} & \sim (\mathbf{0}, \mathbf{\rho^2}) \end{aligned} $$

$$ \begin{aligned} \color{red} P(\mathbf{d}|\mathbf{a};\sigma_g^2,\sigma_b^2)&=(2\pi)^{-N/2}\|\mathbf{C}_d(\sigma_g^2,\sigma_b^2,\mathbf{a})\|^{-1/2}\times exp \left[-\frac{1}{2}(\mathbf{d-Ha})^T\mathbf{C}_d^{-1}(\sigma_g^2,\sigma_b^2)(\mathbf{d-Ha})\right] \\ f(\mathbf{Sa})&= \cdots exp \left[ -\frac{1}{2} \mathbf{a}^T \begin{pmatrix} S_\xi^T & S_\tau^T \end{pmatrix} \begin{pmatrix} \rho_\xi^2 \mathbf{I_M} & 0 \\ 0 & \rho_\tau^2 \mathbf{I_M} \end{pmatrix}^{-1} \begin{pmatrix} S_\xi \\ S_\tau \end{pmatrix} \mathbf{a} \right] \\ &= \cdots exp \left[-\frac{1}{2} \mathbf{a}^T \left( \frac{S_\xi^TS_\xi+\chi^2S_\tau^TS_\tau}{\rho^2} \right) \mathbf{a}\right], \quad \chi^2=\frac{\rho_\xi^2}{\rho_\tau^2}\\ \color{red} P(\mathbf{a};\rho^2)&=(2\pi)^{-M/2}\begin{Vmatrix}\frac{G_\xi+\chi^2G_\tau}{\rho^2}\end{Vmatrix}^{1/2}\times exp \left[-\frac{1}{2} \mathbf{a}^T \left( \frac{G_\xi+\chi^2G_\tau}{\rho^2} \right) \mathbf{a}\right] \end{aligned} $$

$$ \begin{aligned} \color{red}P&{\color{red}(\mathbf{a};\sigma_g^2,\sigma_b^2,\rho^2|\mathbf{d})}=cP(\mathbf{d}|\mathbf{a};\sigma_g^2,\sigma_b^2)P(\mathbf{a};\rho^2)\\ &=\bbox[#A9F5A9] {c(2\pi)^{-(N+M')/2}\|\mathbf{C}_d(\sigma_g^2,\sigma_b^2,\mathbf{a})\|^{-1/2} \begin{Vmatrix}\frac{G_\xi+\chi^2G_\tau}{\rho^2}\end{Vmatrix}^{1/2}} \\ &\quad \times exp \left[-\frac{1}{2}\left((\mathbf{d-Ha})^T\mathbf{C}_d^{-1}(\sigma_g^2,\sigma_b^2,\mathbf{a})(\mathbf{d-Ha}) + \mathbf{a}^T \left( \frac{G_\xi+\chi^2G_\tau}{\rho^2} \right) \mathbf{a} \right) \right] \\ &=\bbox[#A9F5A9]{c(2\pi\sigma_g^2)^{-(N+M')/2}\|\Sigma_d(\gamma^2,\mathbf{a})\|^{-1/2} \|\beta^2(G_\xi+\chi^2G_\tau)\|^{1/2} } \\ &\quad \times exp \left[-\frac{1}{2\sigma_g^2}\left(\bbox[#F5A9BC]{(\mathbf{d-Ha})^T\mathbf{\Sigma}_d^{-1}(\gamma^2,\mathbf{a})(\mathbf{d-Ha}) + \beta^2\mathbf{a}^T ( G_\xi+\chi^2G_\tau ) \mathbf{a} }\right) \right] \\ &=\bbox[#A9F5A9]{c(2\pi\sigma_g^2)^{-(N+M')/2}\|\Sigma_d(\gamma^2,\mathbf{a})\|^{-1/2} \|\beta^2(G_\xi+\chi^2G_\tau)\|^{1/2} } \times exp \left[-\frac{\mathbf{S(a)}}{2\sigma_g^2} \right] \\ &\qquad \qquad \gamma^2=\sigma_b^2/\sigma_g^2;\quad \beta^2=\sigma_g^2/\rho^2;\quad \sigma_g^2\Sigma_d=C_d \\ \end{aligned} $$

$$ \begin{aligned} \bbox[5px, border:2px solid red] {\frac{\partial s(\mathbf{a})}{\partial \mathbf{a}}} &= \frac{\partial \left[(\mathbf{d-Ha})^T\mathbf{\Sigma}_d^{-1}(\gamma^2,{\color{red}\mathbf{a}^i})(\mathbf{d-Ha}) + \beta^2\mathbf{a}^T ( G_\xi+\chi^2G_\tau ) \mathbf{a} \right] }{ \partial \mathbf{a} } = \mathbf{0} \\ &\iff \mathbf{H}^T\Sigma_d^{-1}(\gamma^2,\mathbf{a}^i)(\mathbf{d-Ha^\star})-\beta^2(\mathbf{G_\xi+\chi^2G_\tau})\mathbf{a}^\star=0 \\ &\iff \bbox[#F5A9F2]{ \mathbf{a}^\star(\gamma^2,\beta^2;a^i)=\left[\mathbf{H}^T\Sigma_d^{-1}(\gamma^2,\mathbf{a}^i)\mathbf{H}+\beta^2(\mathbf{G_\xi+\chi^2G_\tau})\right]^{-1}\mathbf{H}^T\Sigma_d^{-1}(\gamma^2,\mathbf{a}^i)\mathbf{d} } \end{aligned} $$

$$ \begin{aligned} S(\mathbf{a})&=(\mathbf{d-Ha})^T\mathbf{\Sigma}_d^{-1}(\gamma^2,{\color{red}\mathbf{a}^i})(\mathbf{d-Ha}) + \beta^2\mathbf{a}^T ( G_\xi+\chi^2G_\tau ) \mathbf{a} \\ S(\mathbf{a}^\star)&=(\mathbf{d-Ha^\star})^T\mathbf{\Sigma}_d^{-1}(\gamma^2,{\color{red}\mathbf{a}^i})(\mathbf{d-Ha^\star}) + \beta^2\mathbf{a^\star}^T ( G_\xi+\chi^2G_\tau ) \mathbf{a^\star} \\ S(\mathbf{a}) & \textit{taylor expansion at :}\; a^\star ;\mathbb{J}\textit{:jacobian matrix;} \mathbb{H}\textit{: Hessian matrix}\\ S(\mathbf{a})&\approx S(\mathbf{a}^\star) + \mathbb{J}(\mathbf{a^\star}) (\mathbf{a-a^\star}) +\frac{1}{2} (\mathbf{a-a^\star})^\mathrm{T} \mathbb{H}(\mathbf{a^\star}) (\mathbf{a-a^\star}); \quad \mathbb{J}(a)|_{a=a^\star}=0 \\ &=\bbox[5px, border:2px solid red]{S(\mathbf{a}^\star)+(\mathbf{a-a^\star})^T \left[ H^T\Sigma_d^{-1}(\gamma^2,{\color{red}\mathbf{a}^i})H+\beta^2(G_\xi+\chi^2G_\tau) \right](\mathbf{a-a^\star}) } \\ ~\\ \end{aligned} $$

$$ \begin{aligned} L&(\sigma_g^2,\gamma^2,\beta^2;{\color{red}\mathbf{a}^i})=\int P(d|a)P(a)~da \\ &=\bbox[#A9F5A9]{(2\pi\sigma_g^2)^{-(N+M')/2}\|\Sigma_d(\gamma^2,{\color{red}\mathbf{a}^i})\|^{-1/2} \|\beta^2(G_\xi+\chi^2G_\tau)\|^{1/2}} \times exp \left[-\frac{1}{2\sigma_g^2} \mathbf{S(a^\star)} \right] \\ &\quad\times \int -\frac{1}{2\sigma_g^2} \left[(\mathbf{a-a^\star})^T \left[ H^T\Sigma_d^{-1}(\gamma^2,{\color{red}\mathbf{a}^i})H+\beta^2(G_\xi+\chi^2G_\tau) \right](\mathbf{a-a^\star})\right] ~d(\mathbf{a-a^\star})\\ &=\bbox[#A9F5A9]{(2\pi\sigma_g^2)^{-(N+M')/2}\|\Sigma_d(\gamma^2,{\color{red}\mathbf{a}^i})\|^{-1/2} \|\beta^2(G_\xi+\chi^2G_\tau)\|^{1/2}} \\ &\quad\times (2\pi\sigma_g^2)^{M''/2} \begin{Vmatrix} H^T\Sigma_d^{-1}(\gamma^2,{\color{red}\mathbf{a}^i})H+\beta^2(G_\xi+\chi^2G_\tau) \end{Vmatrix}^{-1/2} \times exp \left[-\frac{1}{2\sigma_g^2} \mathbf{S(a^\star)} \right] \\ &=(2\pi {\color{#0000FF}\sigma_g^2})^{-(N+M'-M'')/2} \times exp \left[-\frac{1}{2{\color{#0000FF}\sigma_g^2}} \mathbf{S(a^\star)} \right] \times \|\sim\|^{-1/2}~\|\sim\|^{1/2}~\|\sim\|^{-1/2} \end{aligned} $$

$$ \begin{aligned} \bbox[5px, border:2px solid red] {\frac{\partial L(\sigma_g^2,\gamma^2,\beta^2;{\color{red}\mathbf{a}^i})}{\partial \sigma_g^2 }} = 0 & \iff \frac{\partial (2\pi {\color{#0000FF}\sigma_g^2})^{-(N+M'-M'')/2} \times exp \left[-\frac{1}{2{\color{#0000FF}\sigma_g^2}} \mathbf{S(a^\star)} \right] }{\partial \sigma_g^2} \\ & \Rightarrow \sigma_g^2=\frac{s(\mathbf{a^\star})}{N+M'-M''}\\ \end{aligned} $$

$$ \begin{aligned} ABIC({\color{red}\gamma^2},{\color{red}\beta^2};&\sigma_g^2,\mathbf{a}^i)=-2log\left[ L({\color{red}\gamma^2},{\color{red}\beta^2};\sigma_g^2,\mathbf{a}^i) \right]\\ =& (N+M'-M'')log(S(\mathbf{a}^\star)) \\ & + log(\begin{Vmatrix} \Sigma_d( {\color{red} \gamma^2},{\mathbf{a}^i}) \end{Vmatrix}) \\ & - log(\begin{Vmatrix} {\color{red}\beta^2}(G_\xi+\chi^2G_\tau) \end{Vmatrix}) \\ & + log(\begin{Vmatrix} H^T\Sigma_d^{-1}({\color{red}\gamma^2},{\mathbf{a}^i})H+{\color{red}\beta^2}(G_\xi+\chi^2G_\tau) \end{Vmatrix}) + C' \\ ~\\ with&:\\ ~\\ S(\mathbf{a}^\star({\color{red}\gamma^2},{\color{red}\beta^2}))&=(\mathbf{d-Ha^\star})^T\mathbf{\Sigma}_d^{-1}({\color{red}\gamma^2},{\mathbf{a}^i})(\mathbf{d-Ha^\star}) + {\color{red}\beta^2}\mathbf{a^\star}^T ( G_\xi+\chi^2G_\tau ) \mathbf{a^\star}\\ \mathbf{a}^\star({\color{red}\gamma^2},{\color{red}\beta^2};a^i)&=\left[\mathbf{H}^T\Sigma_d^{-1}({\color{red}\gamma^2},\mathbf{a}^i)\mathbf{H}+{\color{red}\beta^2}(\mathbf{G_\xi+\chi^2G_\tau})\right]^{-1}\mathbf{H}^T\Sigma_d^{-1}({\color{red}\gamma^2},\mathbf{a}^i)\mathbf{d} \\ ~\\ \textit{covariance }&\textit{matrix for the model parameters:} \\ C_a({\color{red}\gamma^2},{\color{red}\beta^2}) &=\sigma_g^2\left[\mathbf{H}^T\Sigma_d^{-1}({\color{red}\gamma^2},\mathbf{a}^i)\mathbf{H}+{\color{red}\beta^2}(\mathbf{G_\xi+\chi^2G_\tau})\right]^{-1} \\ \textit{iteratively }&\textit{update initial model:} \\ a_n^i&=a_{n-1}^i+ w(a_{n-1}^\star - a_{n-1}^i) (0 \lt w \lt 1) \\ &~\\ \textit{solution for}&~\gamma^2,\beta^2: \textit{object function:}\,\mathbf{ABIC}(\gamma^2,\beta^2),\textit{or}~\mathbf{S}(\mathbf{a}(\gamma^2,\beta^2))\\ &~\textit{grid_search} \\ &~\textit{neighborhood method} \\ &~\textit{Levenberg-Marquardt}\\ Min:~ABIC & \iff Max: \int P(d|a)P(a)~da \quad \textit{;entropy maximization principle} \\ Min:\quad S(a) & \iff Max: \quad P(d|a)P(a) \quad\quad \textit{;} Max~P(a|d) &~\\ &~\\ \widehat{\mathbf{a}}^{~\star}({\color{red}\sigma_b^2},{\color{red}\rho^2};a^i)&=\left[\mathbf{H}^T C_d^{-1}({\color{red}\sigma_b^2},\mathbf{a}^i) \mathbf{H}+{(\mathbf{G_\xi+\chi^2G_\tau})}/{\color{red}\rho^2}\right]^{-1}\mathbf{H}^T C_d^{-1}({\color{red}\sigma_b^2},\mathbf{a}^i) \mathbf{d} \\ \widehat{C}_a({\color{red} \sigma_b^2},{\color{red} \rho^2}) &=\left[\mathbf{H}^T~C_d^{-1}({\color{red}\sigma_b^2},\mathbf{a}^i)\mathbf{H}+{(\mathbf{G_\xi+\chi^2G_\tau})}/{\color{red}\rho^2}\right]^{-1} \\ \widehat{S}(\mathbf{a}^\star({\color{red}\sigma_b^2},{\color{red}\rho^2}))&=(\mathbf{d-Ha^\star})^T C_d^{-1}({\color{red}\sigma_b^2},{\mathbf{a}^i})(\mathbf{d-Ha^\star}) + \mathbf{a^\star}^T ( G_\xi+\chi^2G_\tau )/{\color{red}\rho^2} \mathbf{a^\star}\\ \widehat{ABIC}({\color{red}\sigma_b^2},{\color{red}\rho^2};&\sigma_g^2,\mathbf{a}^i)\\ = &log(\begin{Vmatrix} C_d( {\color{red} \sigma_b^2},{\mathbf{a}^i}) \end{Vmatrix}) \\ - &log(\begin{Vmatrix} (G_\xi+\chi^2G_\tau)/{\color{red}\rho^2} \end{Vmatrix}) \\ + &log(\begin{Vmatrix} H^T C_d^{-1}({\color{red}\sigma_b^2},{\mathbf{a}^i})H+(G_\xi+\chi^2G_\tau)/{\color{red}\rho^2} \end{Vmatrix}) + C \\ ~\\ \end{aligned} $$

$$ \begin{aligned} u(t)&=\sum_{n=1}^{N}\sum_{q=1}^{Q}\sum_{l=1}^{L} \sum_{k=1}^{K} \mathbf{G}(\overset{nqlk}{\xi},t) \cdot m_{nqlk}*T_l(t-\overset{nq}{t_k}) \\ &+\sum_{n=1}^{N}\sum_{q=1}^{Q}\sum_{k=1}^{K}~\sum_{l=1}^{L}\Delta \mathbf{G}(\overset{nqkl}{\xi},t) \cdot m_{nqlk}*T_l(t-\overset{nq}{t_k})+e(t)\\ u(t)&=\sum_{n=1}^{N}\sum_{q=1}^{Q}\sum_{l=1}^{L} \sum_{k=1}^{K} \mathbf{G}(\overset{nqlk}{\xi},t) \cdot \overset{n}{m_0} \cdot a_{nqlk}*T_l(t-\overset{nq}{t_k}) \\ &+\sum_{n=1}^{N}\sum_{q=1}^{Q}\sum_{k=1}^{K}~\sum_{l=1}^{L}\Delta \mathbf{G}(\overset{nqkl}{\xi},t) \cdot \overset{n}{m_0} \cdot a_{nqlk}*T_l(t-\overset{nq}{t_k})+e(t)\\ u(t)&=\sum_{n=1}^{N}\sum_{q=1}^{Q}\sum_{l=1}^{L} \sum_{k=1}^{K} \mathbf{G}(\overset{nqlk}{\xi},t) \cdot \mu \cdot a_{nqlk}*T_l(t-\overset{nq}{t_k}) \\ &+\sum_{n=1}^{N}\sum_{q=1}^{Q}\sum_{k=1}^{K}~\sum_{l=1}^{L}\Delta \mathbf{G}(\overset{nqkl}{\xi},t) \cdot \mu \cdot a_{nqlk}*T_l(t-\overset{nq}{t_k})+e(t)\\ \color{red} u(t)&=\sum_{n=1}^{N}\sum_{q=1}^{Q}\sum_{l=1}^{L} \sum_{k=1}^{K} \mathbf{G}(\overset{nqlk}{\xi},t) \cdot \mu \cdot a_{nqlk} \cdot \Delta \xi_1 \Delta \xi_2 *T_l(t-\overset{nq}{t_k}) \\ &+\sum_{n=1}^{N}\sum_{q=1}^{Q}\sum_{k=1}^{K}~\sum_{l=1}^{L}\Delta \mathbf{G}(\overset{nqkl}{\xi},t) \cdot \mu \cdot a_{nqlk} \cdot \Delta \xi_1 \Delta \xi_2 *T_l(t-\overset{nq}{t_k})+e(t)\\ \end{aligned} $$

$$ \begin{aligned} \nabla^2 \dot{D}(t,\xi)+e_{\xi} =0 \iff & \mathbf{S_{\xi }a+e_{\xi }=0} \iff \mathbf{G_{\xi }=S_{\xi }^TS_{\xi }} \\ \frac{\partial^2}{\partial t^2}\dot{D}(t,\xi)+e_{\tau} =0 \iff & \mathbf{S_{\tau}a+e_{\tau}=0} \iff \mathbf{G_{\tau}=S_{\tau}^TS_{\tau}} \\ \end{aligned} $$

$$ \begin{matrix} \frac{\partial^2 (\cdots) }{\partial x^2 } & \iff & \frac{1}{c^2} \frac{\partial^2 (\cdots) }{ \partial t^2 } \\ \mathbf{S_{\xi }a} ~ \Rightarrow ~ \mathbf{a^T}\mathbf{G_{\xi }}\mathbf{a} & \iff & \frac{1}{c^2} \mathbf{S_{\tau}a} ~ \Rightarrow ~ \mathbf{a^T}\mathbf{G_{\tau}}\mathbf{a} \\ -\mathbf{a^T} \left( \frac{1}{2\rho_{\xi}^2}\mathbf{G_{\xi}}+\frac{1}{2\rho_{\tau}^2}\mathbf{G_{\tau}} \right) \mathbf{a} & \iff & -\frac{1}{2}~\mathbf{a^T} ~\frac{ \mathbf{G_{\xi}} + (\rho_{\xi}^2/\rho_{\tau}^2) \mathbf{G_{\tau}} }{\rho_{\xi}^2} ~ \mathbf{a} \\ ~ & \rho_{\xi}^2/\rho_{\tau}^2 = 1/c^4 \quad \color{red} & \color{red} ? \end{matrix} $$

$$ \begin{aligned} \dot{D}_q^0(t,\xi) \thickapprox & \sum_{k=1}^K \sum_{l=1}^L a_{qkl}X_k(\xi)T_l(t-t_k) \\ u_j(t)= &\sum_{q=1}^2 \int_s G_{qj} (t,\xi)* \dot{D}_q(t,\xi)~d\xi ~ ; \\ \iff & \sum_{q=1}^2 \int_s \mathbb{G}_{qj}^{FK}(t,\xi)* \dot{\mathbb{M}}_q(t,\xi)~d\xi ; \quad \textit{Zhu's FK GRN is referred to Moment.} \\ \quad & \int_\Sigma \int_t ~ \dot{\mathbb{M}}(t,\xi)~dt~d\xi=M_0 ;\quad \dot{\mathbb{M}} \iff \dot{D} \\ \textit{ let: } & G=\mu \mathbb{G}^{FK} \textit{ then: } \\ \iff & \sum_{q=1}^2 \int_s G_{qj}(t,\xi)* \dot{D}_q(t,\xi)~d\xi ; \\ \quad & \int_\Sigma \int_t ~ \dot{D}(t,\xi)~dt~d\xi=M_0/\mu; \quad \dot{D} \iff \dot{D} \\ ~&~\\ \end{aligned} $$

$$ \begin{aligned} & \dot{D}_q(t,\xi) ~ \textit{ interpolated from } ~ a_{qkl} ~ \textit{, theoretically } \dot{D}_q(t,\xi) \textit{ and } ~ a_{qkl} ~ \textit{ should have} \\ & \textit{same dimensions, so}~ X_k(\xi)\;,\; T_l(t-t_k) \textit{should be dimensionless,} \\ & \textit{ then, we can normalize the base functions as follows: } \\ \end{aligned} $$

$$ \begin{aligned} \int_\Sigma X_k\left(\mathbf{\xi}\right) ~d\mathbf{\xi} = \Delta \xi_1 & \Delta \xi_2 \quad ; \quad \int_t ~ T_l\left(t-t_k\right) ~ ~dt = \Delta t \\ \int_\Sigma \int_t ~ \dot{D}_q^0(t,\xi) ~dt~d\xi &\thickapprox \int_\Sigma \int_t ~ \sum_{k=1}^K \sum_{l=1}^L a_{qkl}X_k(\xi)T_l(t-t_k) ~dt~d\xi \\ &=\sum_{k=1}^K \sum_{l=1}^L a_{qkl} \Delta \xi_1 \Delta \xi_2 \Delta t \iff a_{qkl} ~ \sim \dot{D} \\ \textit{if normalize the base functions as } & \textit{follows:} \\ \int_\Sigma X_k\left(\mathbf{\xi}\right) ~d\mathbf{\xi} = \Delta \xi_1 & \Delta \xi_2 \quad ; \quad \int_t ~ T_l\left(t-t_k\right) ~ ~dt = 1 \\ \int_\Sigma \int_t ~ \dot{D}_q^0(t,\xi) ~dt~d\xi &\thickapprox \int_\Sigma \int_t ~ \sum_{k=1}^K \sum_{l=1}^L a_{qkl}X_k(\xi)T_l(t-t_k) ~dt~d\xi \\ &=\sum_{k=1}^K \sum_{l=1}^L a_{qkl} \Delta \xi_1 \Delta \xi_2 \iff a_{qkl} ~ \sim \overline{D} \\ \end{aligned} $$

$$ \begin{equation} \begin{aligned} \int_{-\infty}^\infty & \exp\left(-\frac 1 2 x^{T} A x \right) \, d^nx=\sqrt{\frac{(2\pi)^n}{\det A}} \\ \int_{-\infty}^\infty & \sqrt{\frac{\det A}{(2\pi)^n}}~\exp\left(-\frac 1 2 x^{T} A x \right) \, d^nx=1 \end{aligned} \end{equation} $$

$$ \begin{equation} f_{\mathbf x}(x_1,\ldots,x_k) = \frac{1}{\sqrt{(2\pi)^k|\mathbf{\Sigma}|}} \exp\left(-\frac{1}{2}({\mathbf x}-{\mathbf \mu})^T{\mathbf \Sigma}^{-1}({\mathbf x}-{\mathbf \mu}) \right) \end{equation} $$

$$ \begin{equation} \begin{aligned} \Sigma^{\mathbf{f=Ax}} &= \mathbf{A} \Sigma^x \mathbf{A}^\mathbf{T} \\ \operatorname{cov}(\mathbf{X}_1 + \mathbf{X}_2,\mathbf{Y}) &= \operatorname{cov}(\mathbf{X}_1,\mathbf{Y}) + \operatorname{cov}(\mathbf{X}_2, \mathbf{Y})\\ \end{aligned} \end{equation} $$

$$ \begin{equation} \begin{aligned} \det(A^{-1}) & = \frac{1}{\det(A)}=\det(A)^{-1} \\ \det(AB) & = \det(A)\det(B) \quad A,B:~square~~matrices \\ \det(cA) & = c^{n}\det(A) \quad\qquad A:~n \times n~matrix \\ \det \begin{pmatrix}A& 0 \\ C& D\end{pmatrix} &= \det\begin{pmatrix}A& B\\ 0& D\end{pmatrix} = \det(A) \det(D) \end{aligned} \end{equation} $$

$$ \mathbf{A} = \begin{bmatrix} \mathbf{A}_{1} & 0 & \cdots & 0 \\ 0 & \mathbf{A}_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \mathbf{A}_{n} \end{bmatrix} $$

$$ \begin{equation} \begin{aligned} \operatorname{det} \mathbf{A} &= \operatorname{det} \mathbf{A}_1 \times \ldots \times \operatorname{det} \mathbf{A}_n, \\ \operatorname{tr} \mathbf{A} &= \operatorname{tr} \mathbf{A}_1 +\cdots +\operatorname{tr} \mathbf{A}_n. \end{aligned} \end{equation} $$

$$ \begin{equation} \begin{pmatrix} \mathbf{A}_{1} & 0 & \cdots & 0 \\ 0 & \mathbf{A}_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \mathbf{A}_{n} \end{pmatrix}^{-1} = \begin{pmatrix} \mathbf{A}_{1}^{-1} & 0 & \cdots & 0 \\ 0 & \mathbf{A}_{2}^{-1} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \mathbf{A}_{n}^{-1} \end{pmatrix}. \end{equation} $$

$$ \mathbf{A} \oplus \mathbf{B} = \begin{bmatrix} \mathbf{A} & \mathbf{0} \\ \mathbf{0} & \mathbf{B} \end{bmatrix} = \begin{bmatrix} a_{11} & \cdots & a_{1n} & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_{m 1} & \cdots & a_{mn} & 0 & \cdots & 0 \\ 0 & \cdots & 0 & b_{11} & \cdots & b_{1q} \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & b_{p1} & \cdots & b_{pq} \end{bmatrix} \\ \bigoplus_{i=1}^{n} \mathbf{A}_{i} = {\rm diag}( \mathbf{A}_1, \mathbf{A}_2, \mathbf{A}_3 \cdots \mathbf{A}_n)= \begin{bmatrix} \mathbf{A}_1 & \mathbf{0} & \cdots & \mathbf{0} \\ \mathbf{0} & \mathbf{A}_2 & \cdots & \mathbf{0} \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{0} & \mathbf{0} & \cdots & \mathbf{A}_n \\ \end{bmatrix}\,\! $$